Hi Ethica!
Is there a way to quickly see how long it took each participant to complete a survey?
For example, we would like to check the reliability of the data of a few participants based on how quickly they filled out each triggered survey (6 a day/1 week). In Kibana we can see individual completion times for each question and we can see when someoone opened the survey and when it was submitted, but not one “duration” variable. Thank you!
Irene
Hey @iivandriel
It’s possible, but it’s a bit tricky. For each response to each survey question, Ethica stores the following variables:
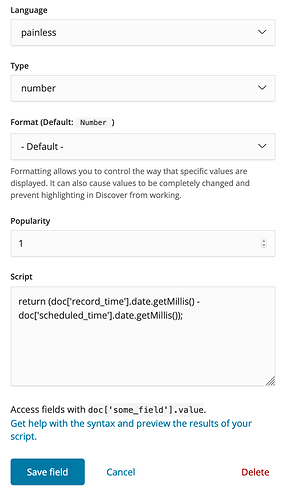
Now the variable you are looking for, duration, is basically Record time - Scheduled time, right? To have this variable, in Kibana you can define a custom scripted field with the following value:
return doc['record_time'].date.getMillis() - doc['scheduled_time'].date.getMillis();
The image below shows the settings I used:
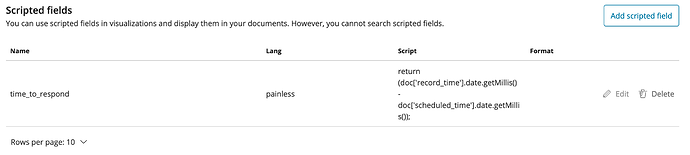
And here is how my index_pattern looks like:
Now if I go to the survey_responses index in Discover tab, I can see the time_to_respond field as well:
Hope it helps,
Mohammad
Thank you, that is insightful.
We would need time of starting survey, not scheduled time. But for that we could replace scheduled time, with for example the record time of the first question?
So record time - record time question ID 1?
You are correct. In that case, instead of subtracting the scheduled time from the record time, you would need to subtract the time the first question was responded from the record time. Here we assume the time the first question was responded is the time the survey was opened.
For this purpose, change the formula to this:
return doc['record_time'].date.getMillis() - doc['resp_time'].date.getMillis();
As Kibana stores each response as a separate record, and the above formula is calculated for each record separately (therefore, for each question separately), the above formula calculates how long after user responded to each question, the survey was completed.
In this case, when you go back to the “Discover” tab of Kibana, you would need to filter the records to show only first question, e.g. “q_id is 1” or any other ID is used for the first question. This will give you the time the participant spent responding the survey.
Hope this helps. Let me know if I should clarify any part of this.
Hi there, I’m trying to compute a duration variable as well but am having trouble with figuring this out – is record_time in the dataset or is it something that I need to request? I am having trouble figuring this out in Kibana. Any help would be appreciated! Thanks so much!
Joanne